According to IBM, 2.5 exabytes of data are generated each day. Every click, like, share and mention generates unlabeled data that can’t be dealt with by traditional statistics. Harnessing this data to deliver personalized user experiences can translate into billions of dollars of incremental revenue: This is the province and promise of deep neural networks (DNNs).
DNNs (multi-layered neural networks or NNs) can churn through massive amounts of unlabeled user data and make highly accurate predictions. Their applications are virtually limitless, from object classification in photos to diagnosing cancer. But for all their power, DNNs have a downside: They can take a long time to train, in part because of the unstable (vanishing or exploding) gradient problem.
Training a NN involves dynamic calculation of a cost value—typically the difference between the actual output and the predicted output based on a set of labelled training data. The cost is lowered by gradually adjusting the weights and biases; this is repeated until the lowest possible cost value is obtained.
The crucial piece in this training process is known as the gradient, which is the rate at which the cost changes with respect to the weight or bias. Larger gradients typically lead to faster learning, while smaller gradients lead to a slower learning process.
The vanishing gradient problem is a difficulty found when using gradient-based training and backpropagation. It results in lengthy training time due to of exponentially reducing gradient steps; additionally, in very deep neural networks, some neurons die because the gradients asymptotically approach zero. As a result, incomplete information passes to the next layer, reducing the accuracy of the result. (The exploding gradient is a related problem that can be experienced under certain conditions.)
But there is a solution to the vanishing gradient problem, and it lies in two key concepts:
Restricted Boltzmann Machine (RBM): An RBM is a shallow, two-layered network—the first layer is visible and the second is hidden. Each node in the visible layer is connected to every layer in the hidden layer; however, no two nodes in the same layer share a connection. The RBM can be thought of as a generalized version of the Boltzmann Machine.
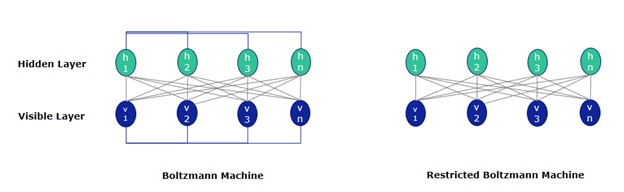
It’s like a two-way translator: In the forward pass, an RBM takes the inputs and translates them into a set of numbers that encodes the inputs. In the backward pass, it takes these numbers and translates them back to form the reconstructed inputs. In both steps, the weights and biases allow the RBM to decipher the relationships between the input features and determine which input features are most important for identifying a pattern.
Through several iterations, an RBM can be trained to reconstruct the input data in three steps:
- In the forward pass, every input is combined with an individual weight and overall bias. The result is passed on to a hidden layer that may/may not be activated.
- In the backward pass, each activation is combined with an individual weight and overall bias. This result is passed to the visible layer for reconstruction.
- At the visible layer, the reconstruction is compared to the original result. The measure used for this is Kullback-Leibler divergence.
These steps are repeated until the error between the actual and reconstructed inputs is deemed acceptably small.
An RBM avoids manual labeling errors because it automatically sorts through data by adjusting weights and biases to extract the key features that reconstruct the input most accurately. The data doesn’t have to be labeled, which makes it useful for recommender systems like online app stores (Google Play, iTunes), e-commerce systems, music recommenders, etc.
Deep Belief Network (DBN): RBMs are the building blocks of DBNs, enabling them to solve the the problem of unstable gradients efficiently. A DBN is a stack of RBMs where the hidden layer of one RBM is the visible layer of the one above it. A DBN’s structure is identical to Multi Layered Perceptron (MLP); however, it’s trained differently. Consider a stack of n RBMs:
- The first RBM is trained to reconstruct its input as closely as possible
- The hidden layer of the first RBM is treated as the visible layer for the 2nd RBM
- The hidden layer of (n-1) is treated as the visible layer of the nth RBM
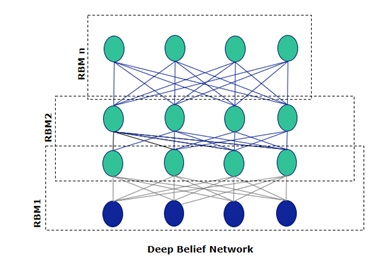
This process is finished when all RBMs are trained; each RBM completes its training by backpropagation before feeding it to the next layer. Because each layer is trained independently, the gradients do not asymptotically reduce. This is the secret sauce to the perfect recipe for avoiding the vanishing gradient problem.
The main difference between DBNs and convolutional neural networks (CNNs) is that each layer of a DBN learns the entire input. On the other hand, early layers in CNNs detect simple patterns, while the latter layers combine them. Consider a CNN that is fed images of animals—the early layers first detect the edges and the latter layers combine these to detect shapes; the final output layer combines the detected shapes to classify the animal into a cat/dog/horse etc.
But a DBN works globally by calibrating the weights and biases until each layer can predict the input as accurately as possible. After the initial training, the RBMs have created a model that can detect inherent patterns in the data; however, the patterns are still unlabeled.
To finish the training, data is labeled and the results are fine-tuned with supervised learning, using small set of labels so that the features can be associated with a name. The weights and biases are altered slightly, resulting in a minor change in the DBNs’ perception of the patterns (this may also lead to a slight increase in accuracy). The set of labeled data is typically small compared to the original dataset.
The benefits of DBNs aren’t limited to shorter training times; they also perform dimension reductions on these massive datasets, making them more comprehensible.
Solving the unstable gradient problem is a major step toward enabling DNNs to extract useful insights from exabytes of unlabeled data. With active research on newer architectures and optimization techniques, we can safely say that deep networks have only just scratched the surface of the AI revolution.
